Collecting Collections - Day 32

Previously on "Collecting Collections"

Method semantics

After gathering a bunch of methods in a table and reading their source or documentation, I had a basic idea for every one of them.I wanted to reduce the amount of necessary concepts to work with a collection. Something like 250 was too much."Maybe if I make a graph, analyzing which method depends on which other I could get a view of the important ones". At least that's what I thought.

(Done with the excellent graph editor: yEd)

As you can see, the complexity is overwhelming. For each method I tried to understand what its intention was and then I tried to describe how it could be done in terms of other methods. In that way I made an edge of the graph for each dependency.

When building this graph I found that some methods had more than one dependency shared with other method. This was specially true for "simetric methods", for example, addLast, addFirst. They had the same dependencies  but added just a small variation to the concept they represent. "Those are the places were missing concepts are! If you can't name something you are condemned to describe it"

That's what my methods were doing! They used other methods as concepts to describe what they do, and the lack of a name was forcing me to repeat descriptions (dependencies).

Two things came to my mind: If I could see a graph like this at any programming level for its dependencies (architecture, class, method, etc) , I would be able to detect this kind of code duplication very easily. Our eye is trained to find this kind of knots. (It could be done automatically, of course). A tool like this on our environments would be great!

I should change the definition of my current methods and try to introduce concepts as needed to simplify the graph

Then, methods like addLast: anObject and addFirst: anObject will depend on at: anOrdinal add: anObject making "first" and "last" an argument. I changed definitions of methods and added a few new ones on the table. The graph simplified a bit (some overlapping lines dissapeared), but it still was a gordian knot. At this point I was imagining how to implement each, but didn't touch a line of code.

Collection concepts

While making the graph and adding new methods I annotated which concepts I needed to describe each method. I wanted to list every concept I needed on my mind. At least which ones were the strongest.

For this task I used MindMup

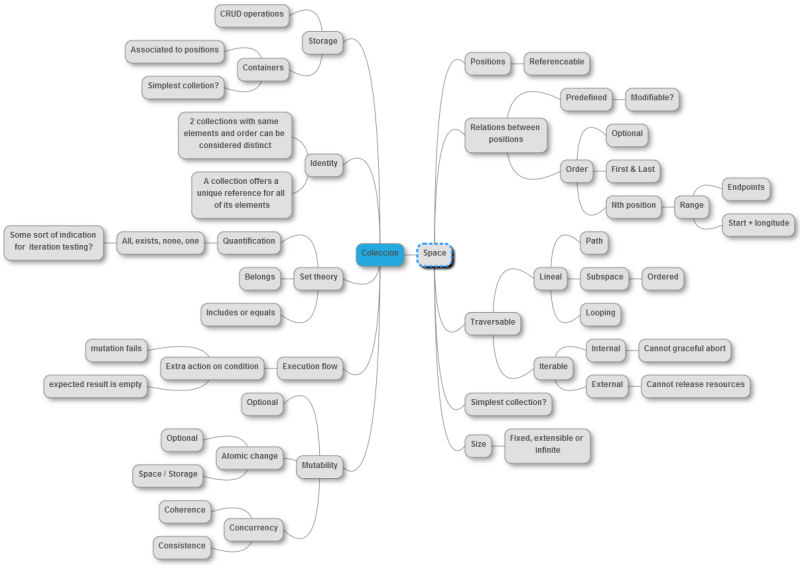
I won't detail each one, but the closest to the collection.

Space:

I found that many methods used, or needed some kind of space were they operated. Specially those involving order. This notion of space is not mathematical but takes some ideas. For example, when iterating an array we normally use an index N. We access the element on position N, and then add 1 to N, and access the N+1 position. We can do this because we are on natural numbers domain and it has an order relation that states that N+1 is the minimum number that satisfies N < N+1. We can traverse and access the array elements in order because we do so using an index that is part of the natural numbers space. The space associated with arrays is a natural number interval space.

What about an unordered collection, let's say a bag. It doesn't have an order. What is its space? For a bag, the elements are stored according to its equality. Equal elements are replaced or rejected, whether they are the same or not. When traversing the bag we don't expect an specific order, but we do expect that we don't pass 2 times over the same equality, and all the equalities are accessed. That means (to me) that the space of the bag is that of the equality. Depending on how the equality relation is defined you define how many positions the space have. For example, if you define the equality to be always true. You would have a one position space, where only one element could be put on the bag. When traversing the bag you want to visit every equality present on the bag. The objects stored there serve as representants.

So depending on the space, there were relations that the method used, or not. If I could find a way to abstract this concept I could add meaningful operations where there were none because the type of collection didn't contemplate it.

Storage:

Some operations were just to use the collection as a place to keep things. Those operations could be classified as CRUD operations. And were no so different from SQL insert, delete, select and update. In one way or another, the intention was very similar. This gives me the idea that every "whole" as an abstract concept should have these basic abstract operations. Whenever you have a whole/part relationship you will want to add, remove, modify or check an part of the whole.

Identity:

When using collections we retain references to them as a way to keep some form of identity and history of the whole. The collection as a reference enables you to access one thing, but having the ability to interact with many (each element). Doing so the operations done on the collection are shared among all of their referants. Also meaning that while you retain the reference to the collection the elements will be there. For example, if you want to model the relationship between a father and its childs you make a collection for the father and put all the childs in. You, then, have two identities, the father and the collection. Adding to the collection means more childs to the father. You modify the collection as a way to express the relationships.

An alternative will be to express every relationship between father and child. The collection defined in this way by comprehension will be the elements that meet that relationship. You know one identity (the father) and many other (the relationships). However it seems that its easier for us as programmers (at least OO Programmers) to treat collections as manipulable identities instead. (Probably because an identity can have behavior?)

Mutability:

Another important aspect of collections is that the majority are mutable (at leas the basics). There are non mutable versions, or concurrent versions. But to me, that means that is easier for us to program thinking in linear execution of object modifications rather than parallel non mutating object transformations. However, if parallel computing continues to grow as is growing now, we'll probably have to modify our sources because there are some assumptions there (yes there! on the collections) that will not be real.

Execution flow

The last concept or aspect that got my attention was that (specially on Smalltalk) there were 2-in-1 methods like selectThenDo, or detectIfNone. At first I thought that they were just a lazy's programmer method. "They don't want to call select and do everytime! I'm sure"

However when building the graph I realized that having selectAndDo as a concept served to simplify the graph. Now other methods can reuse that method reducing its own complexity, requiring less steps to do what they do.

What about detectIfNone. I thought it was just checking for the result of detect. However, if the collection can have any object inside, you can't compare the result with anything to assume that is "none". The property of "not being in the collection" is not something you can check outside the collection. Is something that only the collection can answer you.

So the collection has to help you in directing the execution flow when the operations you make in it have more than one outcome.